思维毒点的新概念

除了知识点、难点、难点难点，考虑到不同人思考上存在有不同程度的漏洞，新定义一个毒点的概念，用来指示某个学习者要所有知识当中，让它思维陷入难以言说的困境的知识。¹

例子

之前那个糖命名的知识现在不能确定是不是毒点了，所以下面是三个新例子。²

离心泵的$NPSH$净正吸入压头（汽蚀余量）与$H_{\rm g}$安装高度

图 离心泵安装高度示意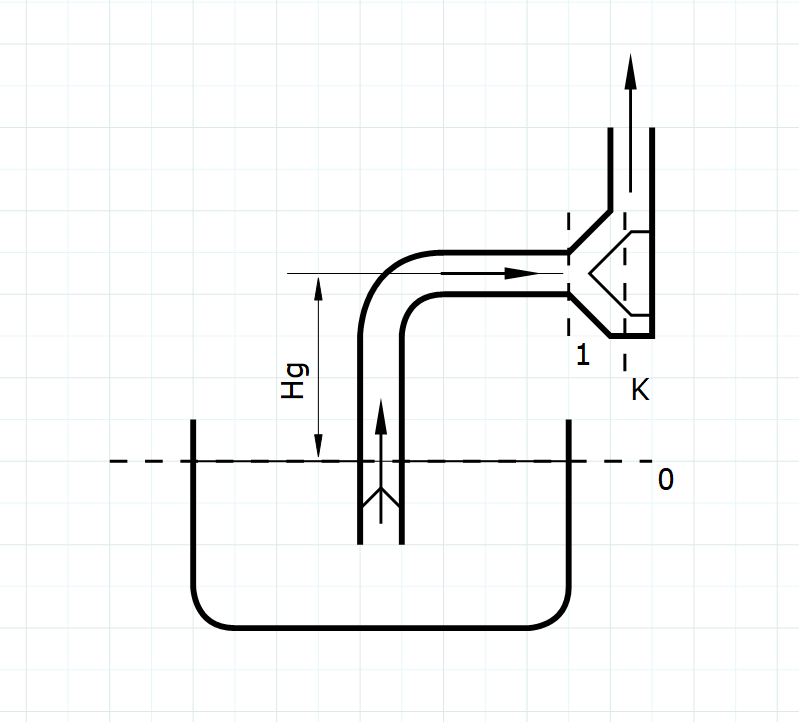

必须汽蚀余量$NPSH_\rm{r}$或$\Delta h_\rm{r}$，其含义为入口处1与最低静压能处K之间某些量的差值（入口处静压头与动压头的和与K处静压头的差，由实验测量得到）。

$$ z_{\rm1}+\dfrac{p_{\rm1}}{\rho g}+\dfrac{u^2_{\rm1}}{2g}=z_{\rm K}+\dfrac{p_{\rm K}}{\rho g}+\dfrac{u^2_{\rm K}}{2g}+H_{\rm f,1-K} $$ $$ \Delta h_{\rm r}=\dfrac{p_{\rm1}}{\rho g}+\dfrac{u^2_{\rm1}}{2g}-\dfrac{p_{\rm K}}{\rho g}=z_{\rm K}-z_1+\dfrac{u^2_{\rm K}}{2g}+H_{\rm f,1-K} $$

不用机械能表示是有道理的，因为确实汽蚀余量表示的差，是一个非常非常规的定义。

安装高度对入口处机械能有影响。³

$$ 0+\dfrac{p_0}{\rho g}+0=H_{\rm g}+\dfrac{p_1}{\rho g}+\dfrac{u^2_1}{2g}+H_{\rm f}$$

于是可以建立起安装高度与$E_{\rm K}$的关系。

$$ H_{\rm g}=\dfrac{p_0}{\rho g}-\dfrac{p_1}{\rho g}-\dfrac{u^2_1}{2g}-H_{\rm f}=\dfrac{p_0}{\rho g}-\dfrac{p_{\rm K}}{\rho g}-\Delta h_{\rm r}-H_{\rm f} $$

汽蚀发生时，静压能小于饱和蒸汽压，而气化，因此有最大安装高度

$$ H_{\rm{g,max}}=\dfrac{p_0}{\rho g}-\dfrac{p_{\rm V}}{\rho g}-\Delta h_{\rm r}-H_{\rm f} $$

允许安装高度会在最大安装高度上增加0.3m左右，而实际安装高度又是允许安装高度的1.1~2.0倍。

毒还由于教材上一个概念有效汽蚀余量$\Delta h_{\rm a}$的影响，思维过程容易卡住。

这个问题的解决只需要依靠记忆代替推理即可，因为它属于STEM中TE方向的内容，属于不具有很强自然逻辑的知识。

管路的特性曲线$H-q_{\rm V}$

图 管路示意图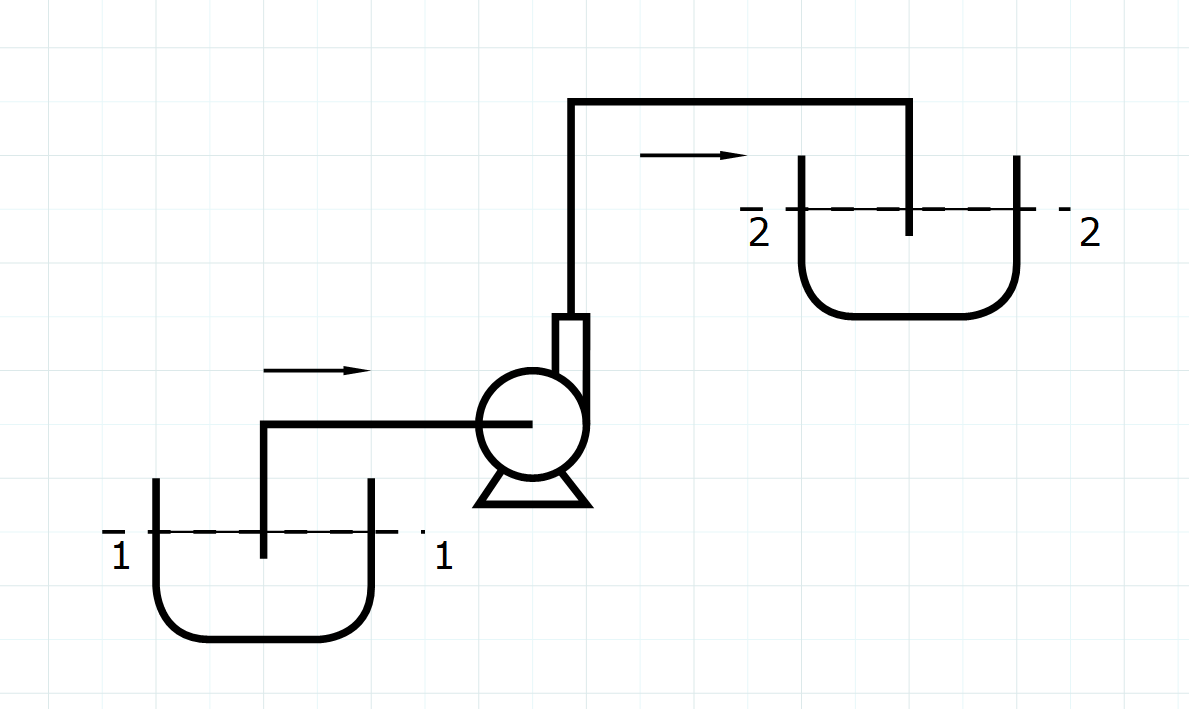

1处到2处建立伯努利方程。⁴

$$ z_1+\dfrac{p_1}{\rho g}+H=z_2+\dfrac{p_2}{\rho g}+\sum H_{\rm f}$$

由于容器内压和位置通常不变，所以位压头与静压头合并成常数项$H_0$。

计算总压头损失的公式从计算总机械能损失的公式推得，但是计算$\sum h_{\rm f}$通常以流速$u$作变量，而这里是体积流量$q_{\rm V}$。

$$ \sum H_{\rm f}=(\xi\dfrac{l+l_{\rm e}}{d^5}+\dfrac{\zeta}{d^4})\dfrac{8q^2_{\rm V}}{\pi^2g}=kq^2_{\rm V}$$

于是得到管路特性曲线方程：

$$ H=H_0+kq^2_{\rm V} $$

管路特性曲线的含义，如果没有示意图是很难联系起来的。事实上示意图给出的入口和出口流体力学参数，加上管路上直管和各管件，就是管路的工作条件，因此可以这么说：管路特性曲线是管路为了达到设定的工作条件，需要泵提供的压头。

等效率曲线

泵的特性曲线、特性参数满足比例定律，并且在实际运用中也认为当转速改变不超过20%时效率基本不变，但是这个说法的含义是，在小范围改变转速时可以认为泵的最高效率、最高效率区不变。事实上，转速减小，$H-q_{\rm V}$左下收缩，最高效率下降的同时最高效率区左移。

连接具有相同效率的点的曲线为等效率曲线，其方程为等效率方程。在讨论这个问题时，认为$H-q_{\rm V}$上由$H$和$q_{\rm V}$确定的一点，具有同样确定的$n$和$\eta$。

由比例定律：

$$ \dfrac{q_{\rm V,1}}{q_{\rm V,2}}=\dfrac{n_1}{n_2}\qquad \dfrac{H_1}{H_2}=\left(\dfrac{n_1}{n_2}\right)^2 $$ $$ H=Kq^2_{\rm V} $$

由上面的描述可知，两转速对应的泵特性曲线，与管路特性曲线相交得到的两个工作点，由于它们不具有相同效率，因而不能用比例定律相互求算。这是个初学时，由于没有啃下难点而很容易造成的误解，这也是毒点。

图 等效率曲线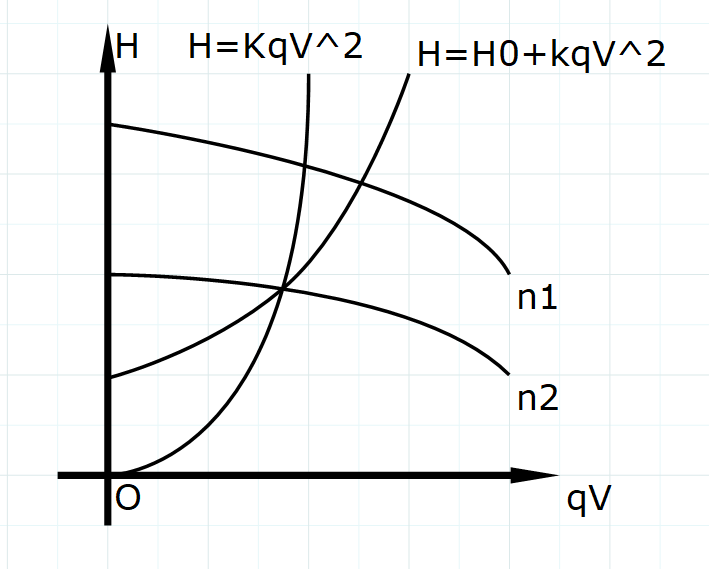

未完待续

接下来是毒+难的基础知识点举例。感觉之前学的算法估计是没学前置知识并且又毒又难的知识点。